Understand Inverse Trig Like a BAND 6 Student - with practice questions

Is inverse trigonometry confusing you like crazy?? Fear not! We are going to break down this topic step by step together so you can ACE it in your next exam.

a year ago • 3 min read

By Manoj Arachige

While inverse trigonometry may sound complex, like all things, you will be able to easily ace it with enough hours of practice! In this blog, we'll dive into inverse trigonometric functions, explore their graphs, unravel key relationships, and prove essential properties to ace your exams.

Defining and Sketching the Inverse Trigonometric Functions

Recall a function only has an inverse function if it is a ONE-TO-ONE. So functions like parabolas must have their domain restricted to a one-to-one in order for it to have a defined inverse function. Trigs are no different.

Inverse trig functions are created by restricting the domain of the o.g functions and then finding the subsequent inverse. You need to memorize what these functions look like and the restrictions on their domain and range.

As shown in the graph, sin⁻¹(x) is defined for -1 ≤ x ≤ 1 and takes values in the range -π/2 to π/2.

As seen above, cos⁻¹(x) is defined for -1 ≤ x ≤ 1 and takes values in the range 0 to π.

Tan⁻¹(x) covers the entire range of real numbers, from -π/2 to π/2, creating a "S" shaped curve.

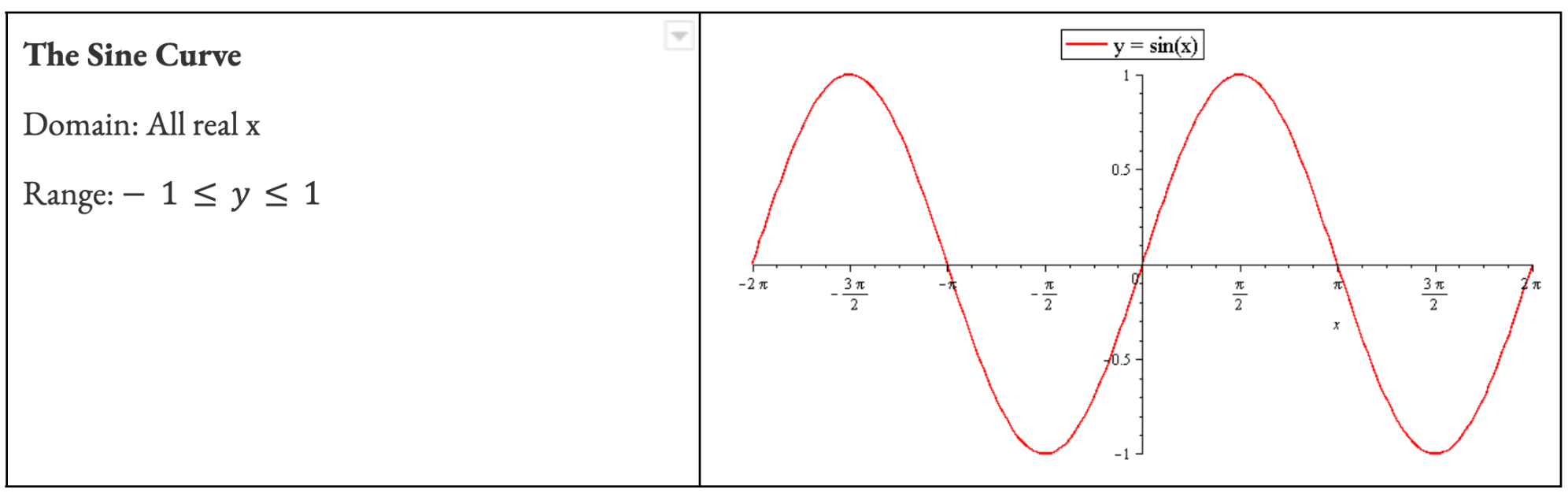
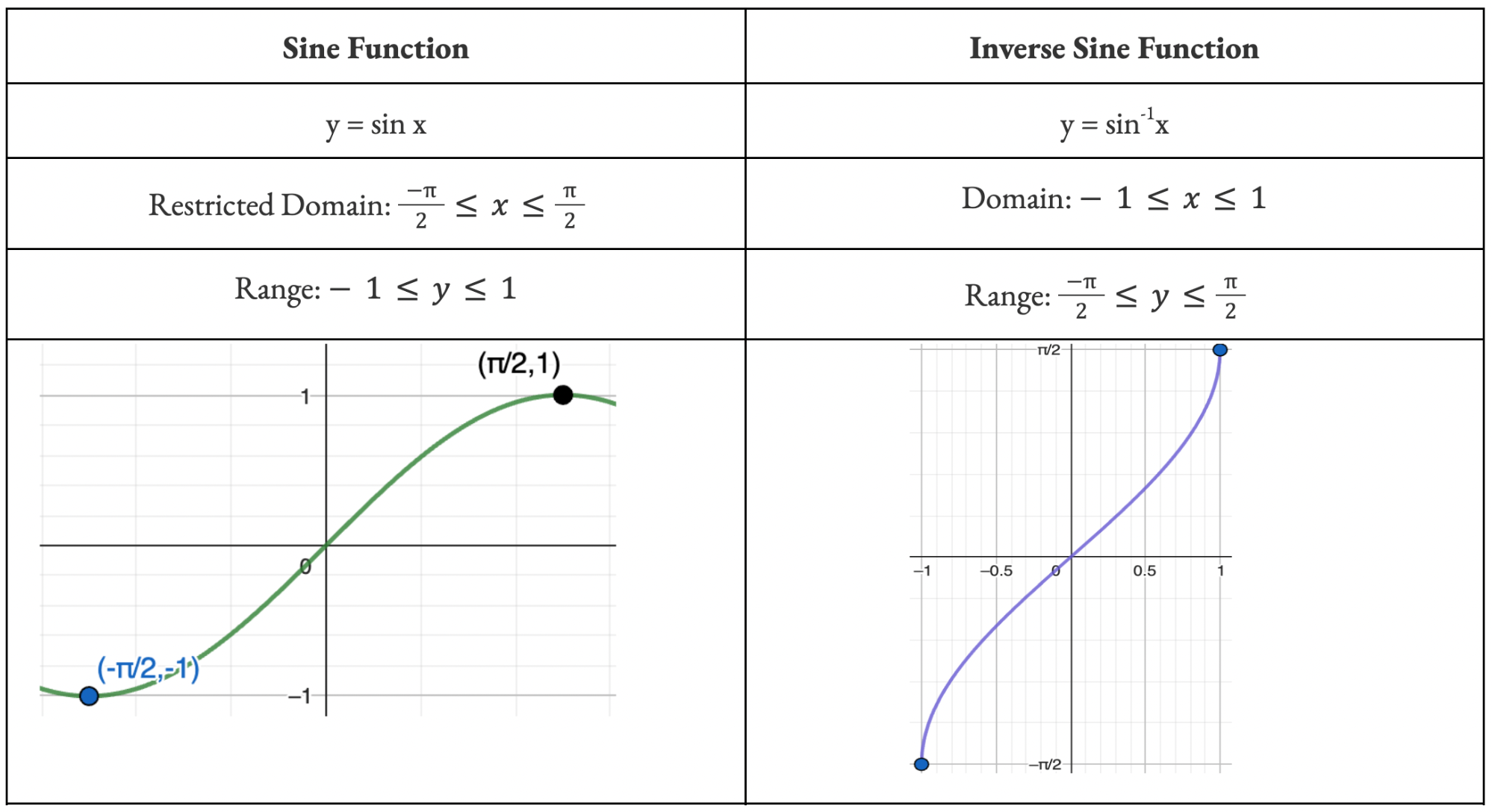
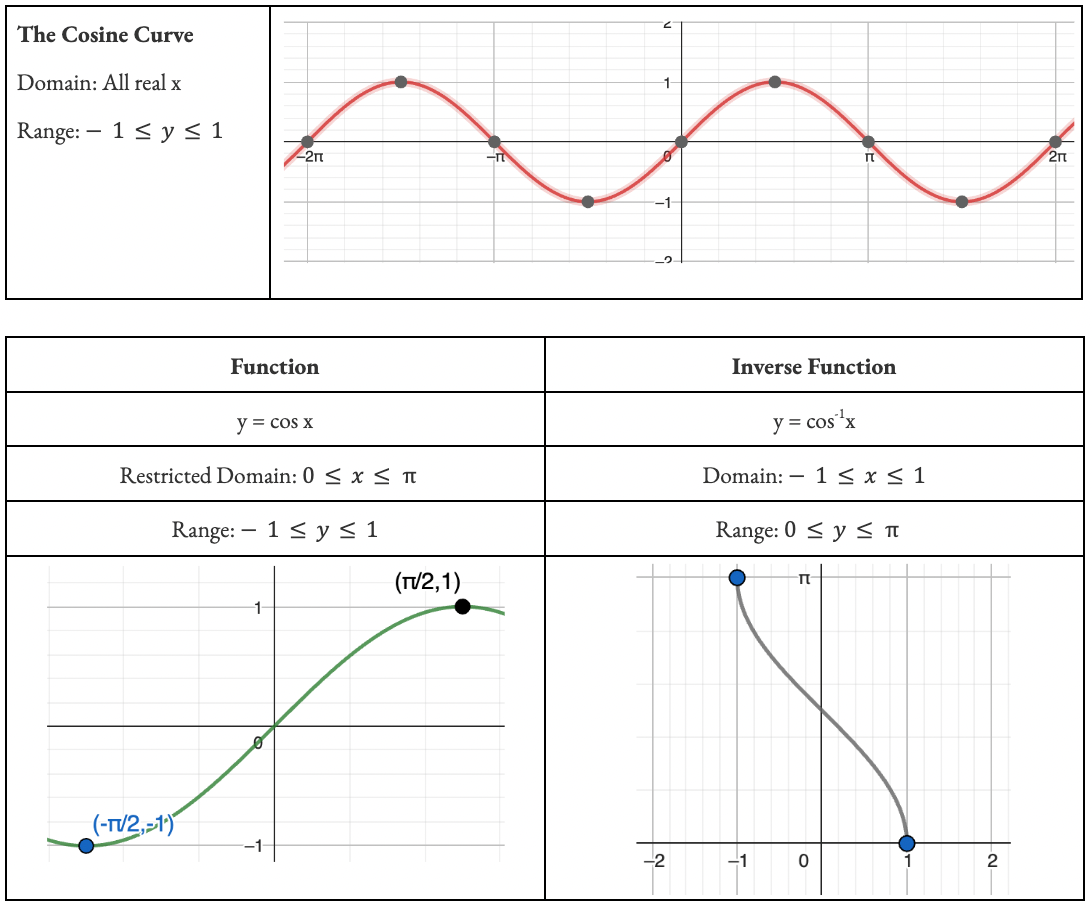
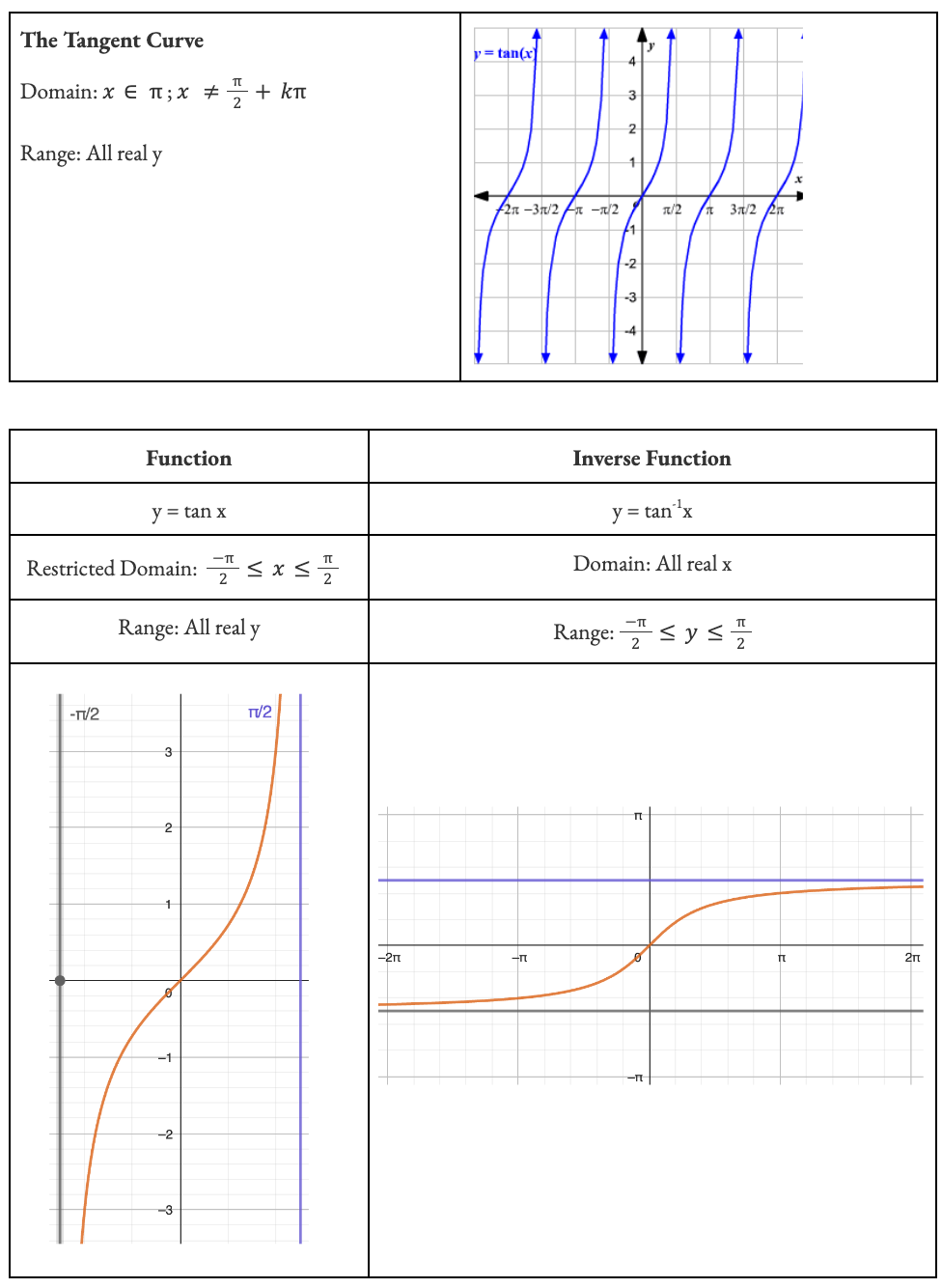
Standard Practice Questions (the ones that will defs show up in exams)

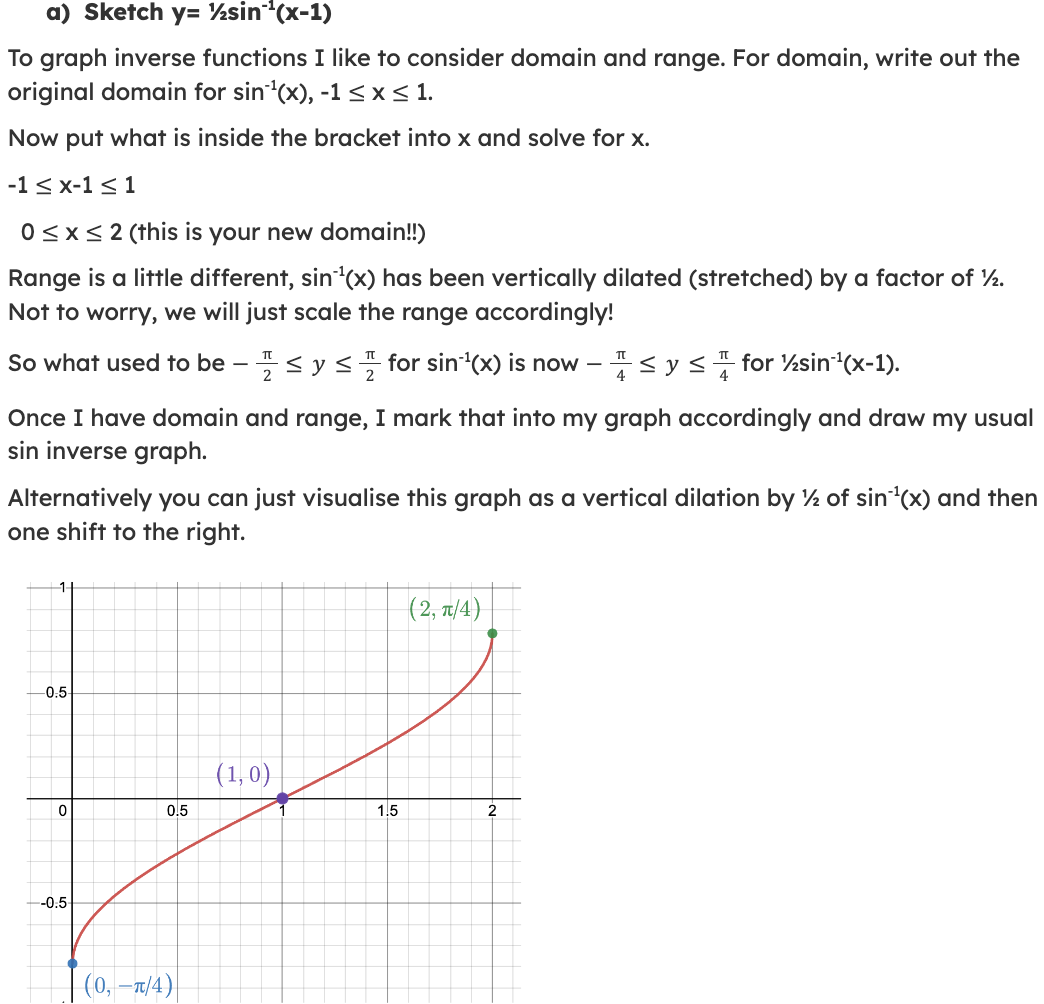
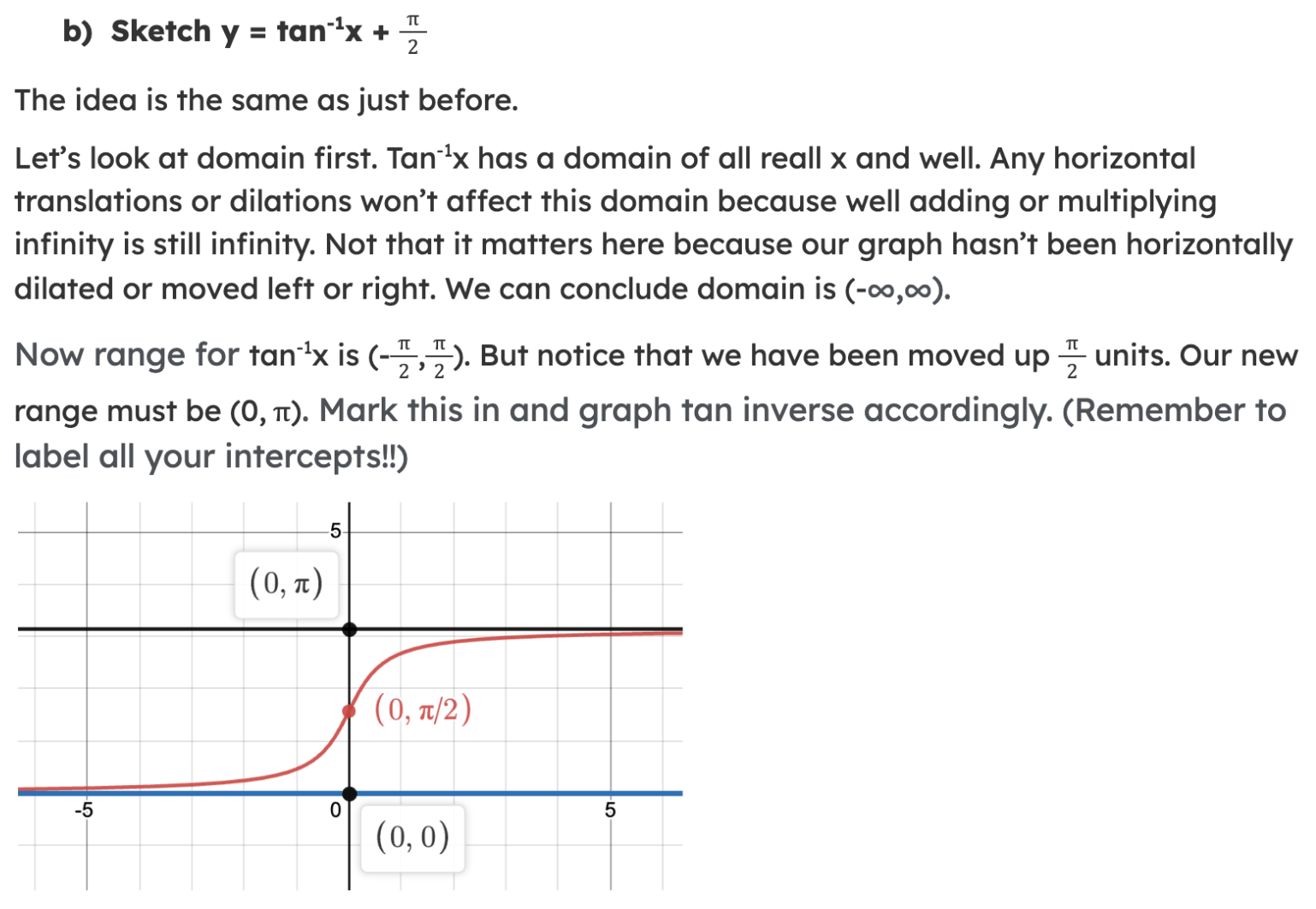
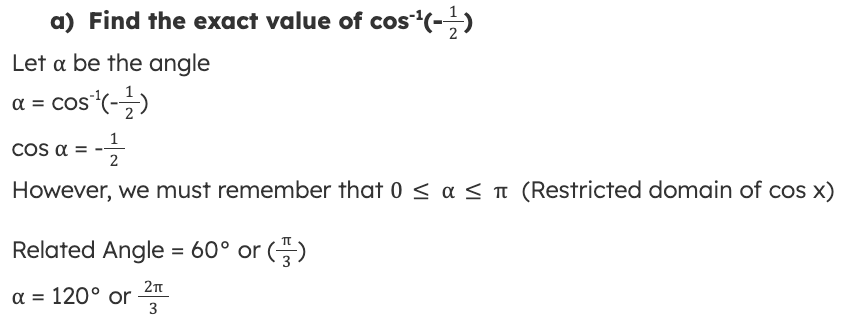
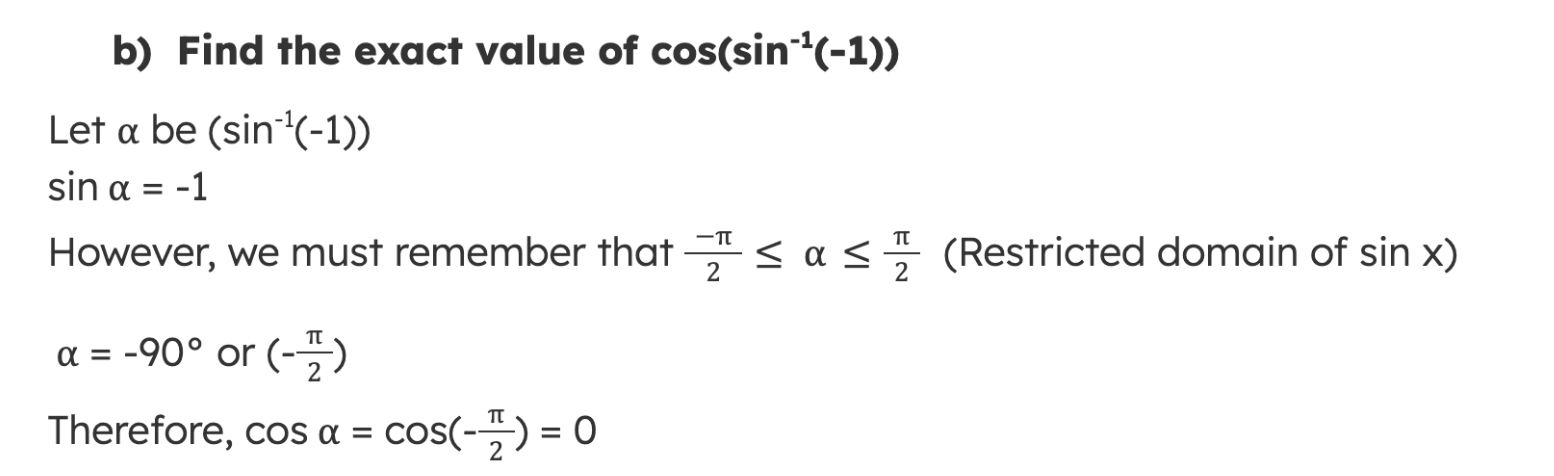
The domain remains the same as all real x, whilst the range changes to (0, Pi).

Key Identities

To master inverse trigonometry, it's crucial to understand and apply key properties. Lucky for you we have compiled it all here in one spot:

Now lets have a feel of how these properties work.

Example Questions using Inverse Properties

My final Study Tips for scoring a BAND 6 in Maths

Practice Regularly:
Consistent practice is key to improving your mathematics skills, no matter what topic you find yourself doing. Solve a variety of problems, especially those from past papers.
Understand Concepts:
Don't simply memorize how to do certain questions; understand the underlying concepts behind finding the correct answer. Knowing why and how a formula works will help you apply it effectively.
Use Visual Aids:
As seen above with the graphs, use visual aids to grasp complex concepts. It makes learning a topic such as inverse trigonometry much easier to grasp.
Don’t Be Afraid to Seek Help:
Not everything clicks with everyone the same way! If you're stuck on a topic, don't hesitate to ask your teacher or a tutor for assistance. They can provide valuable insights and clarification.

Want more personalized guidance to drastically improve your math marks? A private tutor can make the biggest difference!

Find your tutor

Written by KIS Academics Tutor for HSC, Martin Tai. Martin is currently studying a Bachelor of Health Science at ANU on path to study postgraduate medicine. Martin is an experienced tutor with phenomenal reviews from his past KIS Academics students. You can view Martin's profile here and request him as a tutor.