Together, we will look at financial applications of sequences and series and then tackle real-world financial decisions like home loans, savings accounts, car loans, and superannuation. Consider this your Band 6 study guide to ace the financial maths segment of your exam.
Financial Applications of Sequences and Series
Before we delve into financial applications, let's recap the basics.
A sequence is a list of numbers arranged in a specific order, while a series is the sum of the terms in a sequence.

Using Geometric Sequences for Financial Analysis
Geometric sequences are handy for modelling situations involving exponential growth and decay, which can be seen in real-world applications such as finance. For instance, consider investments, loans, and savings accounts.
Key Idea:
In financial applications, the common ratio (r) represents the growth or decay factor, usually expressed as a decimal.
Example Question 1 - Savings Account
Sam invests $5,000 in a savings account with an annual interest rate of 4%. How much will he have in the account after 5 years?
N.B The initial $5000 is referred to as the principal (P)

Example Question 2a - Car Loan
Suppose Rachel takes out a car loan with a 12% annual interest rate, and you plan to make monthly payments of $300. How many months will it take to pay off a $15,000 car loan?
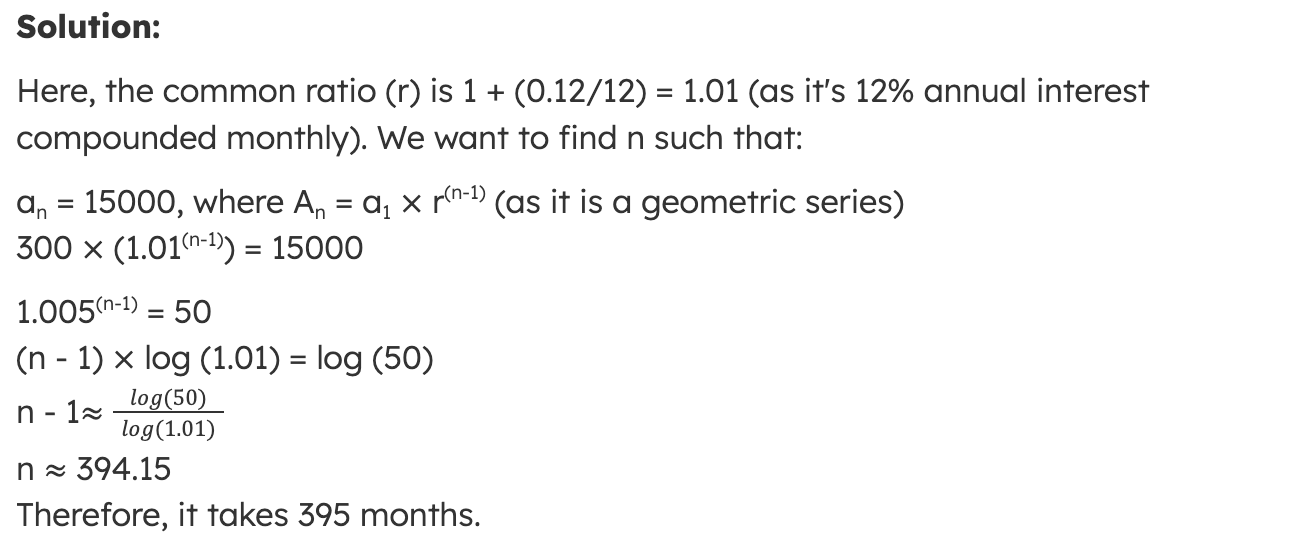
Example Question 2b - Car Loan
Myles takes out a loan of $34000 to buy a car. He will repay the loan in five years, paying 60 equal monthly payments, beginning a month after he takes out the loan. Interest is charged at 6% per annum, compounded monthly. Find how much the monthly instalment should be, to the nearest cent.

Example Question 3 - Home Loan
Liam takes out a loan of 200000 on the 1st of January 2016 to buy a house. He will repay the loan in monthly instalments of $2200. Interest is charged at 12% p.a., compounded monthly.
- Find a formula for the amount owing at the end of n months.
- How much will he owe after 5 years?
- How long does it take to repay
i) Half the loan?
ii) The full loan?
N.B: 12% p.a. = (0.12/12) = 0.01 = 1% per month = therefore the rate of interest used should be 1.01.

Example Question 4 - Superannuation
Tom invests $250 at the end of each month into his superannuation fund at 6% per annum, starting in 2007 and making his last payment in December 2045. How much will he have at the end of 2045.

Want more personalised guidance to drastically improve your math marks? A private tutor can make the biggest difference!
Written by KIS Academics Tutor for HSC, Martin Tai. Martin is currently studying a Bachelor of Health Science at ANU on path to study postgraduate medicine. Martin is an experienced tutor with phenomenal reviews from his past KIS Academics students. You can view Martin's profile here and request him as a tutor.






