While inverse trigonometry may sound complex, like all things, you will be able to easily ace it with enough hours of practice! In this blog, we'll dive into inverse trigonometric functions, explore their graphs, unravel key relationships, and prove essential properties to ace your exams.
How to Define and Sketch the Inverse Trigonometric Functions?
Recall a function only has an inverse function if it is a ONE-TO-ONE. So functions like parabolas must have their domain restricted to a one-to-one in order for it to have a defined inverse function. Trigs are no different.
Inverse trig functions are created by restricting the domain of the o.g functions and then finding the subsequent inverse. You need to memorize what these functions look like and the restrictions on their domain and range.
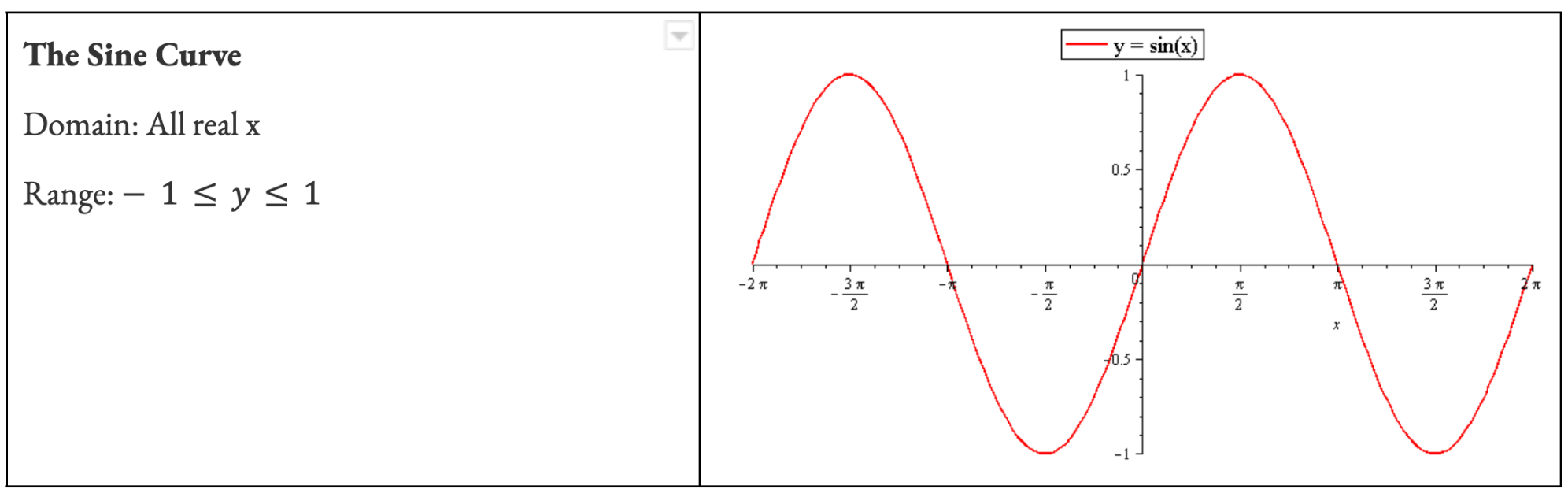
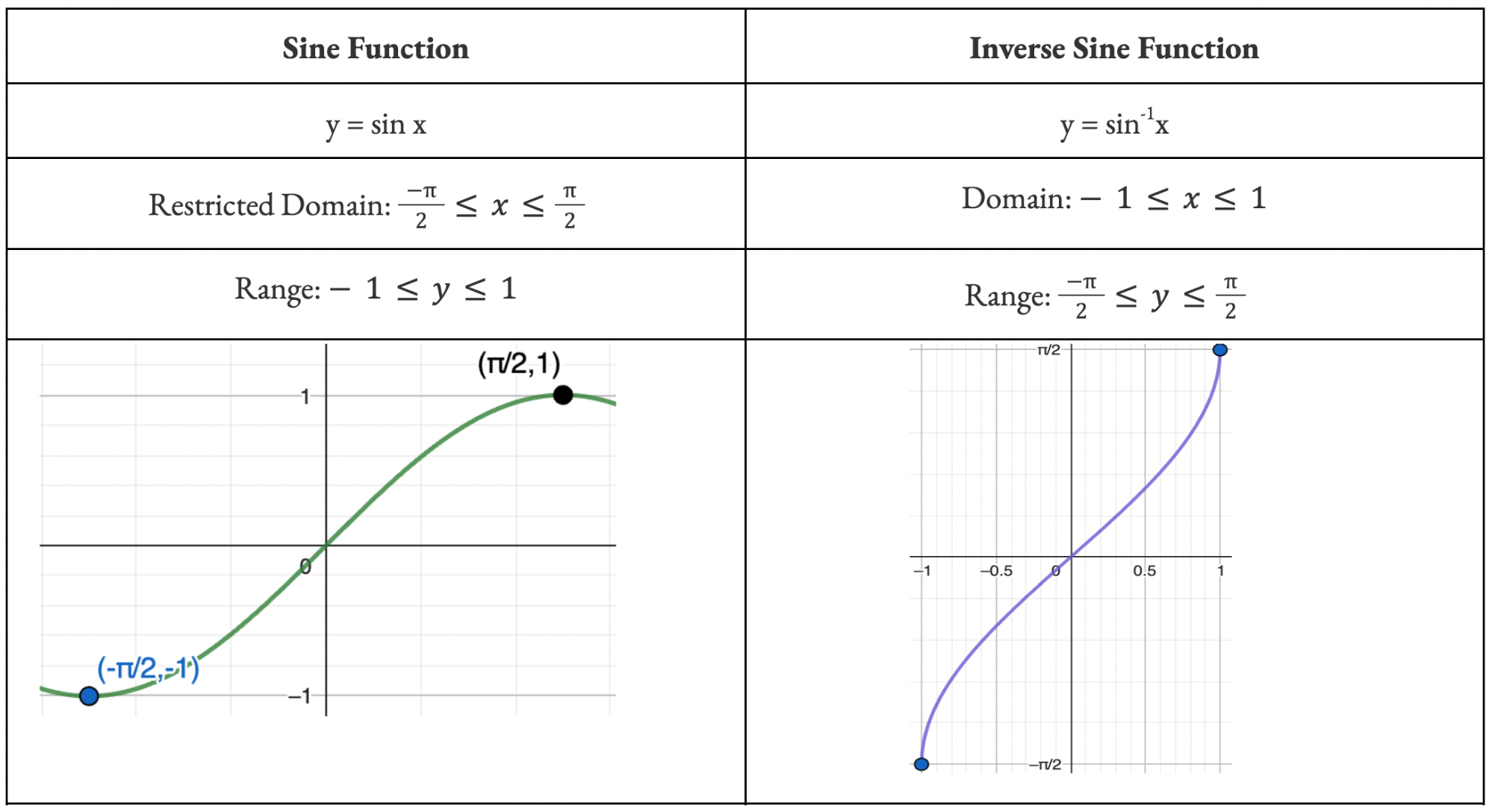
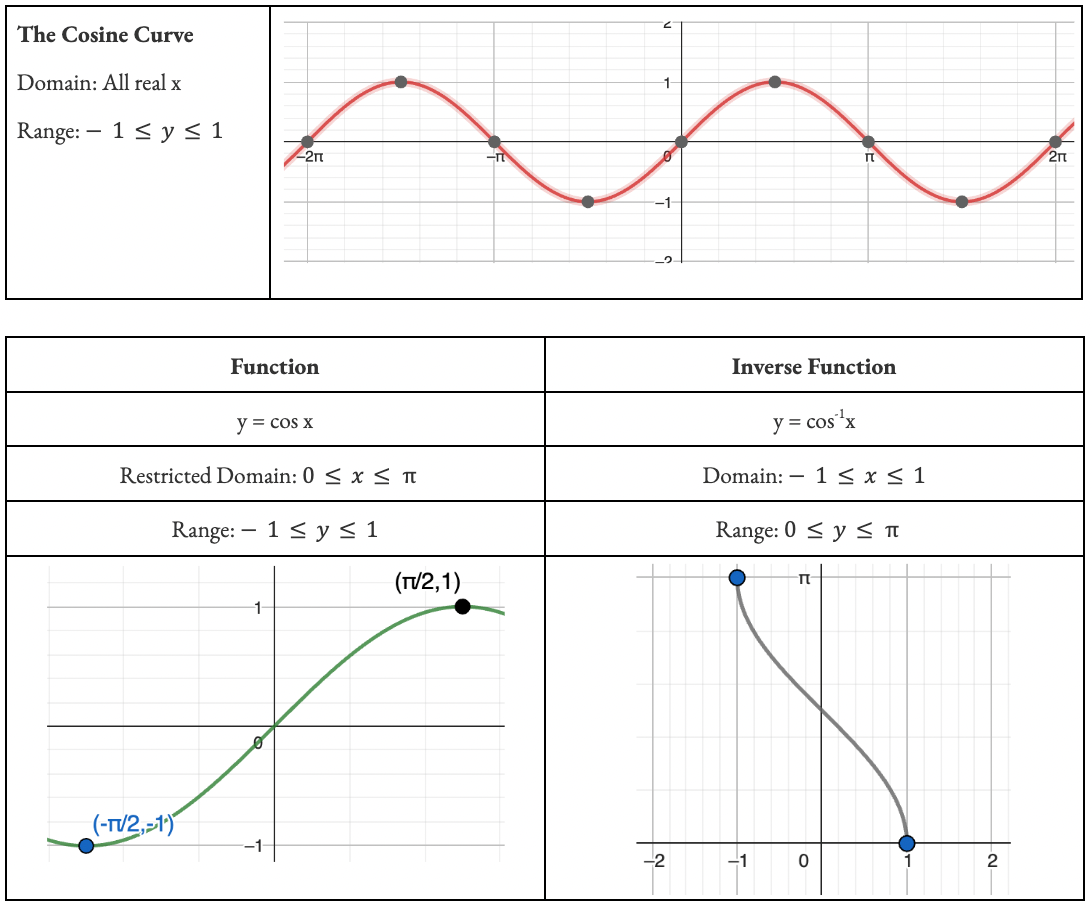
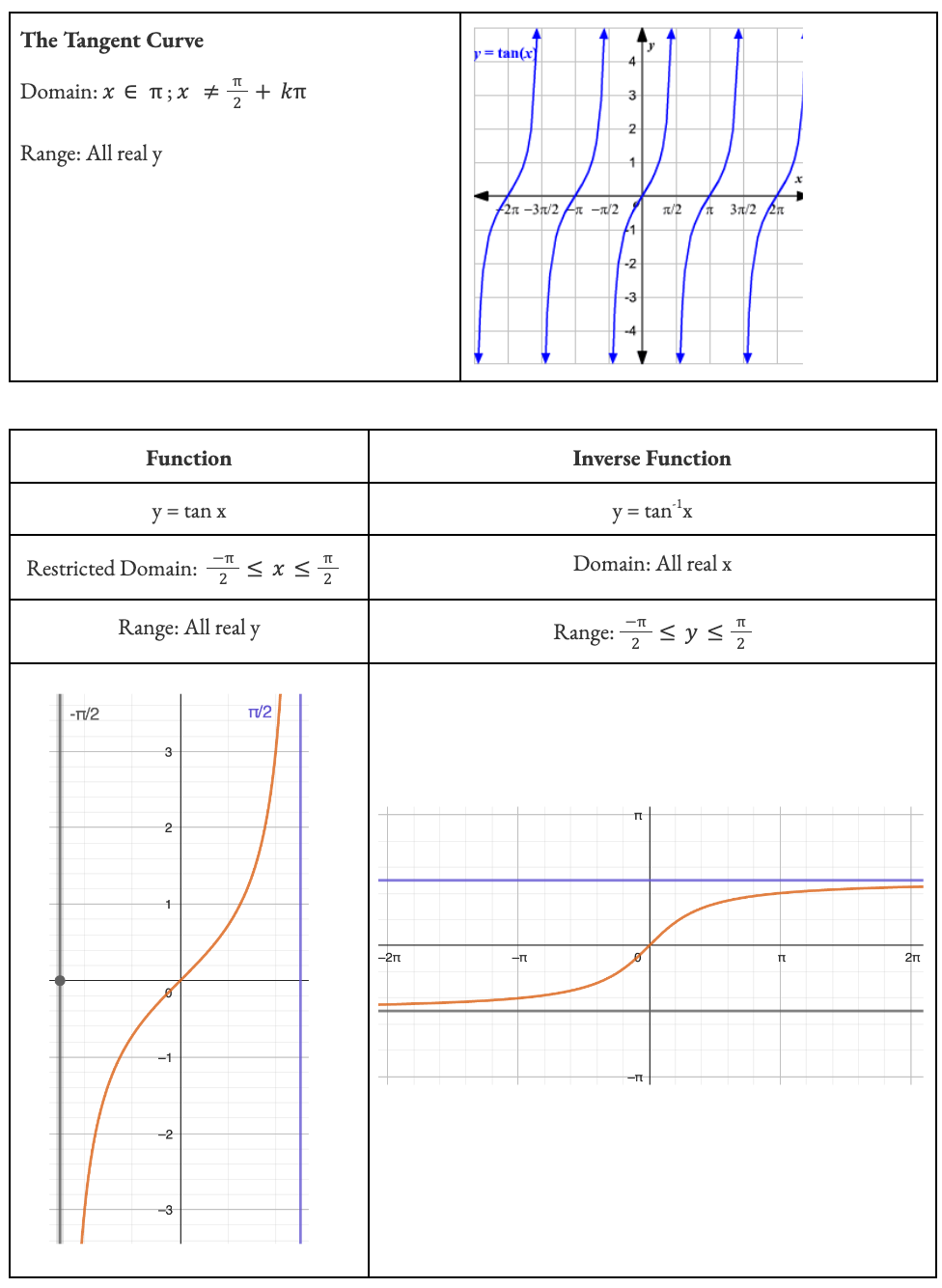
What are the Standard Practice Questions?
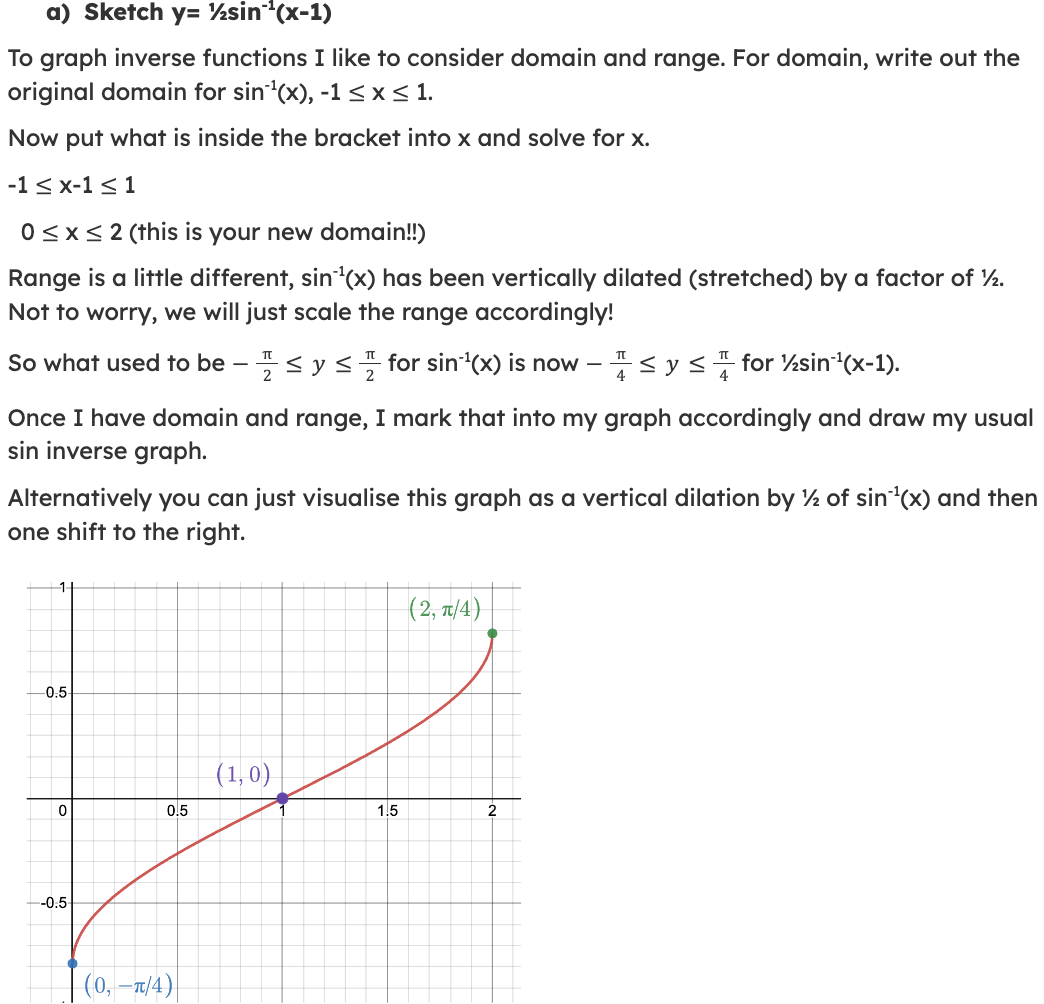
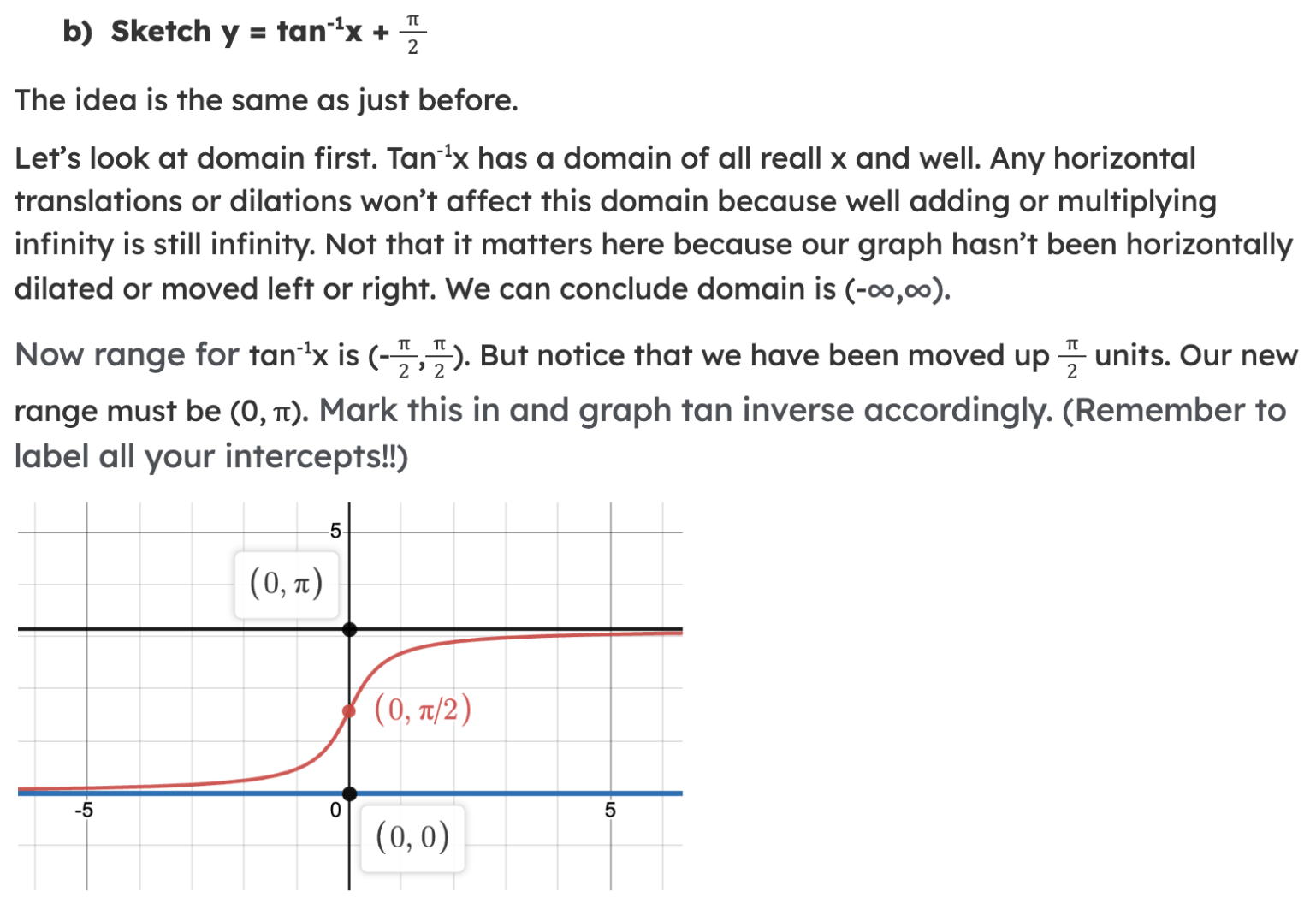
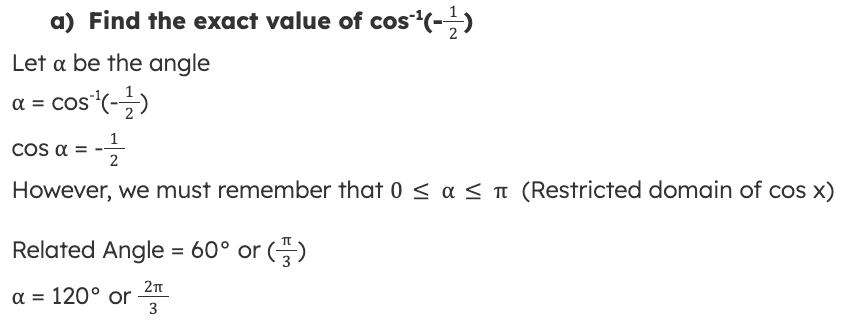
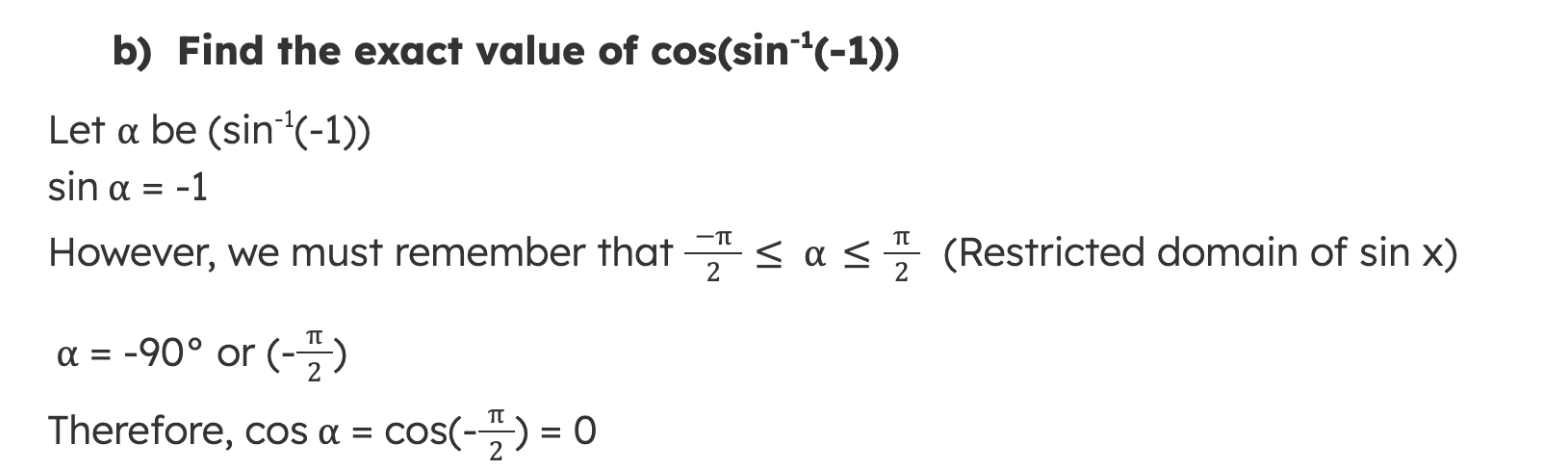
What are the Key Identities?
To master inverse trigonometry, it's crucial to understand and apply key properties. Lucky for you we have compiled it all here in one spot:
Now lets have a feel of how these properties work.
Example Questions using Inverse Properties
Final Study Tips
- Practice Regularly:
Consistent practice is key to improving your mathematics skills, no matter what topic you find yourself doing. Solve a variety of problems, especially those from past papers. - Understand Concepts:
Don't simply memorize how to do certain questions; understand the underlying concepts behind finding the correct answer. Knowing why and how a formula works will help you apply it effectively. - Use Visual Aids:
As seen above with the graphs, use visual aids to grasp complex concepts. It makes learning a topic such as inverse trigonometry much easier to grasp. - Don’t Be Afraid to Seek Help:
Not everything clicks with everyone the same way! If you're stuck on a topic, don't hesitate to ask your teacher or a tutor for assistance. They can provide valuable insights and clarification.
Conclusion
Want more personalized guidance to drastically improve your math marks? A private tutor from KIS Academics can make the biggest difference! For more Math practice questions, check these articles out:
Manoj Arachige
Manoj Arachige
Manoj Arachige
FAQs
What are the types of questions that can be tested?
- Sketching and labelling inverse trig graphs
- Applying and proving identities/transformation properties
- Using inverse trig in practical contexts or geometric problems
What are the key mistakes to avoid?
- Mixing up range restrictions or applying an inverse trig function outside its domain
- Failing to use or justify principal values (ranges)
- Not expressing answers in the proper form (e.g. radians when required)
- Forgetting to check solutions fit within required domains
Written by KIS Academics Tutor for HSC, Martin Tai. Martin is currently studying a Bachelor of Health Science at ANU on path to study postgraduate medicine. Martin is an experienced tutor with phenomenal reviews from his past KIS Academics students. You can view Martin's profile here and request him as a tutor.
What Our Students & Parents Say
Real reviews from students and parents across all our tutoring programs — collected from Google, Trustpilot, and more.
